📄 06 - SET-3 (Trains Relative Speed), p.1

⭐ Basic Concepts

** 📌 1) Relative Speed – Key Concept**

• Relative Speed applies only to problems where two objects are moving towards or away from each other.
• In relative speed problems, when two objects move in the same direction, it's called a chasing scenario. When they move in opposite directions, it's called a meeting scenario.

**📌 2) Rules for solving Relative Speed problems **

• Relative Speed (Like a Magnet)
• 2 objects moving in the same direction → Subtract the 2 Speeds.
• 2 objects moving in the opposite direction → Add the 2 Speeds.
• Remember: (S)ame → (S)ubtract

🎯Problem 1:

A train takes 11 seconds and 10 seconds to cross 2 men who are walking in the same direction of the train at the speed of 6 km/hr and 5 km/hr respectively. Find the speed of the train.

==(A) 16 km/hr ==
(B) 200 km/hr
(C) 18 km/hr
(D) 17 km/hr

• In Relative Speed type, when two cases are given in the question, start the sum by equating the quantity (usually the passing distance 'D') that remains constant in both cases.
• In Relative Speed type, when a train and two men pass each other, start the sum by equating the quantity (train length) that remains constant in both cases (the train passing each man separately).

🎯Problem 2:

A train overtakes two boys who are walking in the opposite direction in which the train is going at the rate of 6 km/h and 12 km/h and passes them completely in 36 seconds and 30 seconds respectively. What is the length of the train?

(A) 120 m
==(B) 300 m ==
(C) 140 m

When substituting values separately into the L.H.S/R.H.S of an equation, the equation's units must be considered while solving, because the units do not cancel out with those units on the other side of the equation.

🎯Problem 3:

Two trains are moving in the same direction at the speeds of 42 km/hr and 84 km/hr and their lengths are 320 metres and 380 metres respectively. What is the time taken (in seconds) by faster train to cross the slower train?

==(A) 60 ==
(B) 80
(C) 90
(D) 120

• When a train passes a non-lengthy object such as a man, tree, or pole, the passing distance D = the length of the train.
• When a train passes a lengthy object such as a bridge, platform, or another train, the passing distance D = the length of the lengthy object + the length of the train.
• When solving an equation with different units, convert all units to the specified unit in the answer.

🎯Problem 4:

Two trains are moving in the same direction at the speeds of 35 km/hr and 71 km/hr. The time taken by faster train to cross a man sitting in the slower train is 48 seconds. What will be the length (in metres) of the faster train?

(A) 540
(B) 420
==(C) 480 ==
(D) 660

🎯Problem 5:

Two metro trains 150 m long are moving in opposite directions. They cross each other in 15 seconds. If one is moving thrice as fast as the other, what is the speed of the faster metro train?

(A) 70 km/hr
==(B) 54 km/hr ==
(C) 60 km/hr
(D) 72 km/hr

🎯Problem 6:

Two trains 150 m and 120 m long respectively moving from opposite directions cross each other in 10 secs. If the speed of the second train is 43.2 km/hr, then the speed of the first train is

==(A) 54 km/hr ==
(B) 50 km/hr
(C) 52 km/hr
(D) 51 km/hr

Page 51:
When cancelling m/s units on both sides of an equation, the result will be in km/hr.

🎯Problem 7:

Ratio between length of trains A and B is 3:5. Speed of train A is 72 km/h and that of train B is 54 km/h & they are running opposite to each other. If train A crosses train B in 16 seconds, then find length of train B.

==(A) 350 m ==
(B) 250 m
(C) 450 m
(D) 150 m
(E) 320 m

Page 52:

• When ratios are given in the question and if you need to find specific quantities, assigning a variable (e.g., 'x') to one or both parts of the ratio can help to solve the problem.
• When simplifying a number in a fraction by canceling common factors, if the next part of the number becomes too small to divide by the factor, place a zero in the quotient before continuing the simplification.

🎯Problem 8:

Renu was sitting inside train A, which was travelling at 50 km/h. Another train, B, whose length was three times the length of A crossed her in the opposite direction in 15 seconds. If the speed of train B was 58 km/h, then the length of train A (in metre) is :

(A) 210
(B) 180
(C) 160
(D) 150

🎯Problem 9:

A train travelling at 44 km/h crosses a man walking with a speed of 8 km/h in the same direction, in 15 seconds. If the train crosses a woman coming from the opposite direction in 10 seconds, then what is the speed (in km/h) of the woman?

(1) 10.5
(2) 10
(3) 9
(4) 8

• In Relative Speed type, when two cases are given in the question, start the sum by equating the quantity (usually the passing distance 'D') that remains constant in both cases.
• In Relative Speed type, when two cases have the same passing Distance 'D', and their corresponding Time values and one Speed value are given in the question, you can find the unknown Speed by inversing the Time Ratio to get the Speed Ratio. Then, use this Speed Ratio to set up a Proportion using the Relative Speeds to find the unknown Speed. Note that one Speed value must be given in the question to find the unknown Speed.

🎯Problem 10:

A train X travelling at 60 kmph overtakes another train Y, 225 meter long, and completely passes it in 72 seconds. If the trains had been going in opposite directions, they would have passed each other in 18 seconds. The length (in meter) of X and the speed (in kmph) of Y are, respectively:

(1) 245 and 45
(2) 245 and 54
(3) 255 and 36
(4) 255 and 40

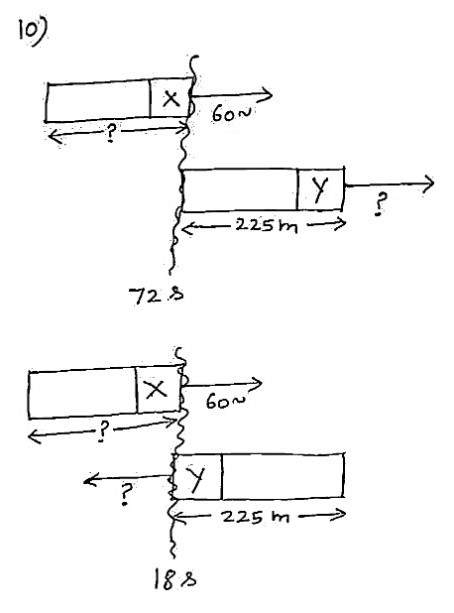
Method 1: Same Distance Relative Speed Method

Method 2: Same Distance Ratio Method

• In Relative Speed type, when two cases have the same passing Distance ‘D’, and their corresponding two Time values and one Speed value are given in the question, we can find the unknown Speed by inversing the Time Ratio to get the Speed Ratio.
• Then, use this Speed Ratio to set up a Proportion using the Relative Speeds to find the unknown Speed. Note that one Speed value must be given in the question to find the unknown Speed.

!350